Сумма углов любого четырехугольника составляет 360 градусов. Это фундаментальное свойство евклидовой геометрии, которое справедливо для всех типов четырехсторонних фигур, независимо от их формы и особенностей.
Содержание
Доказательство теоремы о сумме углов
Существует несколько способов доказать, что сумма углов четырехугольника равна 360°:
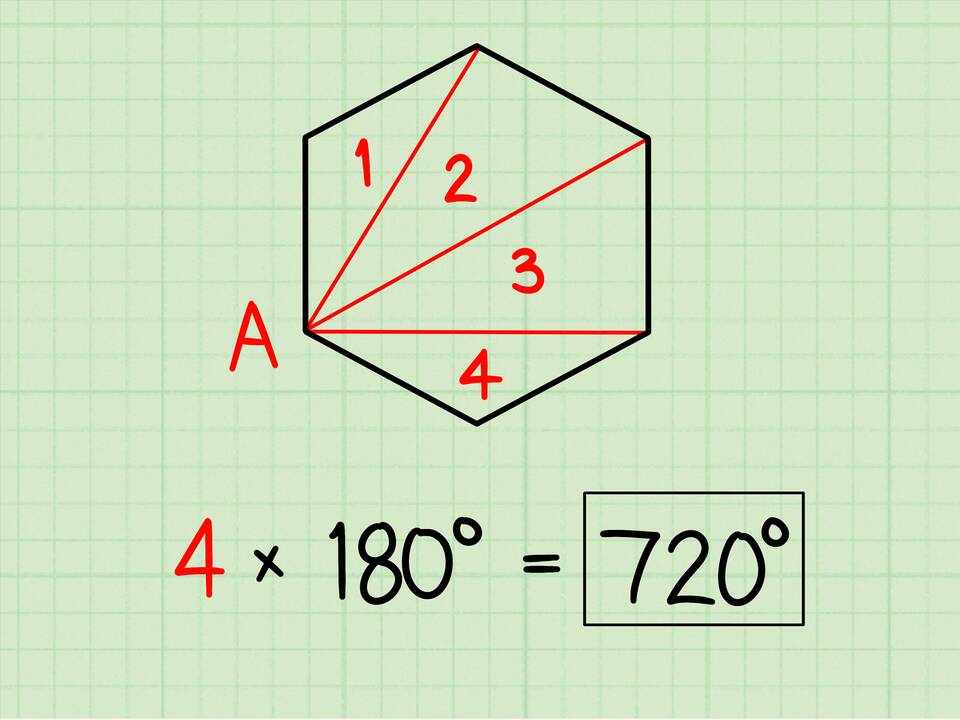
Метод разбиения на треугольники
- Проведите диагональ в четырехугольнике, разделяя его на два треугольника
- Сумма углов каждого треугольника равна 180°
- Два треугольника дают: 180° × 2 = 360°
Алгебраический метод
- Обозначьте углы четырехугольника как A, B, C, D
- Сумма внутренних углов: A + B + C + D
- Сумма внешних углов любого многоугольника равна 360°
- Для каждого угла: внутренний угол + внешний угол = 180°
- 4 × 180° - 360° = 360°
Примеры для различных типов четырехугольников
| Тип четырехугольника | Особенности углов |
| Прямоугольник | Все углы по 90°: 90° × 4 = 360° |
| Ромб | Противоположные углы равны |
| Трапеция | Сумма углов при каждой боковой стороне 180° |
| Произвольный выпуклый четырехугольник | Углы различны, но сумма 360° |
Практическое применение свойства
Знание суммы углов четырехугольника используется:
- В архитектуре и строительстве
- При проектировании технических деталей
- В геодезических измерениях
- При решении геометрических задач
- В компьютерной графике и 3D-моделировании
Интересные следствия из теоремы
- В четырехугольнике не может быть более трех острых углов
- Если три угла прямые, то четвертый тоже прямой (прямоугольник)
- Сумма внешних углов четырехугольника также равна 360°
Историческая справка
Это свойство было известно еще древнегреческим математикам. Евклид в своих "Началах" (III век до н.э.) использовал разбиение многоугольников на треугольники для доказательства подобных теорем.
Заключение
Сумма углов любого четырехугольника, независимо от его вида и свойств, всегда составляет 360 градусов. Это фундаментальное геометрическое свойство находит широкое применение в различных областях науки и техники, а его понимание необходимо для решения множества практических задач.